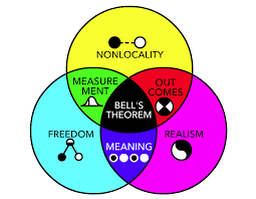
What does Bell's Theorem mean?
The problem Bell turned into a theory was published late in the day for particle physics, in 1964; you'll see in the story why it is that science gets itself tangled up in the maths, why scientists find it so hard to step away from conventionally accepted principles, and why nonlocality has proved to be such a pain in the ass. Einstein, Podolsky and Rosen conspired to quash nonlocal phenomena in the 1930s giving rise to what's now known as the EPR Paradox. Rants raged.
Bell's Theorem means that everything gets to be non-local. No exceptions. Except for the exception in real life, when we get to experience direct contact with those furnishings and beings in our immediate spacetime. Even then, though, we still may be left with room for doubt - doubt which Einstein famously disliked. For something to exist and be nonlocal, it has to be a beable, which I read to rhyme with 'beagle' for a while, and to be a beable means it is able to be present in a version of observable reality. Being Beable is also dependent, with some deference to the Uncertainty Principle, on asymmetry - inequalities, in other words - which leans heavily towards the argument for uniqueness being underpinned by the U.P..

The Scholarship study from which most information has been taken for this post comments on the Multiverse as follows:
A formulation of a version of the many-worlds interpretation which includes, in addition to the wave function, some local beables, was presented in a recent paper, but it was found by the authors to be non-local. The question of whether a many-worlds (or relational) approach can be taken advantage of to create a local (and empirically viable) theory thus remains open — as does the question of how seriously one should take a theory of this type, should it be successfully constructed. For prediction regarding the likely outcome of such a theory being proposed, see below*.
Bell's Theorem itself sets up a paradox, for in defending nonlocality it also insists on locality being a fundamental necessity and true to our observation of reality, it is. To cover this, there exists a "no-conspiracy assumption", described thus: "The "no conspiracy" assumption... is strictly speaking just that — an additional assumption (beyond locality) on which the derivation of Bell-type inequalities rests."
What can Bell's Theorem do for me?
The direct causes (and effects) of events are near by, and even the indirect causes (and effects) are no further away than permitted by the velocity of light, In relativistic terms, locality is the requirement that goings-on in one region of spacetime should not affect — should not influence — happenings in space-like separated regions."
But they do, influence that is, and we see evidence of this all the time in our relationships with people, situations, opportunities and random events. We experience synchronicity because of this influence, and know instinctively that a Thing in one region of spacetime can have a direct - nonlocal - effect on anOther. For these, and other reasons, we cannot definitively dismiss an integration of quantum mechanics into classical physics as being a sound, affordable probability.
Bell has contributed, as much as anyone in the quantum field, to the belief that reality is a flexible commodity. That he avoids Everett in his interpretations is perhaps unsurprising but that leap of faith is waiting to be made by someone else, unafraid to face the *Ninja gauntlet of fierce opposition* that would undoubtedly ensue. Meanwhile, what his Theorem can do for us is to shore up the certainty that we do have an effect, no matter what we do, on the world at large, and since we have no idea what may come from those effects, we might as well trust that all is as it's meant to be, and get on with the Purpose, whatever that is.
 RSS Feed
RSS Feed
